Uma das coisas interessantes do processamento geoespacial é a variedade de ferramentas, e as maneiras de colocá-las juntas podem produzir resultados surpreendentes.
Um membro da comunidade na lista de usuários do PostGIS perguntou: “Existe uma maneira de dividir um polígono em subpolígonos de áreas mais ou menos iguais?”
O desenvolvedor do PostGIS, Darafei Praliaskouski, respondeu e forneceu uma solução funcional que é absolutamente brilhante ao combinar as partes do kit de ferramentas do PostGIS para resolver um problema bastante complicado. Ele disse:
Do jeito que eu vejo, para qualquer tipo de polígono:
- Converte um polígono em um conjunto de pontos proporcionais à área por ST_GeneratePoints (quanto mais pontos, mais bonito será, acho que 1000 está ok);
- Decida quantas partes você gostaria de dividir em (ST_Area (geom) / max_area), seja K;
- Para cada cluster, pegue um ST_Centroid (ST_Collect (point));
- Alimente esses centróides em ST_VoronoiPolygons, que lhe dará uma máscara para cada parte do polígono;
- Com o ST_Intersection do polígono original e cada célula dos polígonos de Voronoi você obterá uma boa divisão do seu polígono em K partes.
Vamos dar um passo de cada vez para ver como funciona.
Usaremos o Peru como polígono de exemplo, ele tem uma boa concavidade, o que o torna um pouco mais complicado do que um polígono com “forma comum”.
CREATE TABLE peru AS SELECT * FROM countries WHERE name = 'Peru'
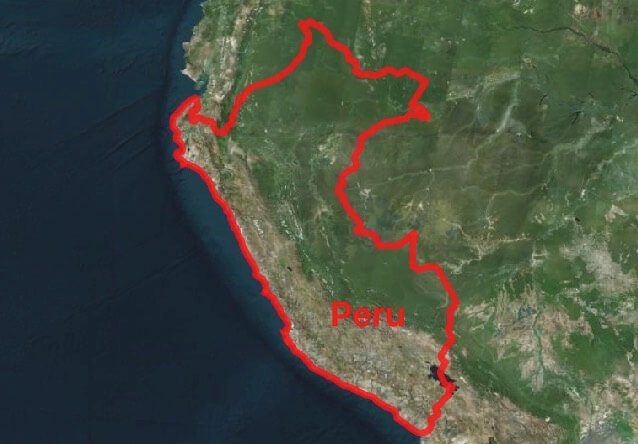
Agora crie um campo de pontos que preencha o polígono. Em média, cada ponto colocado aleatoriamente acaba “ocupando” uma área igual dentro do polígono.
CREATE TABLE peru_pts AS SELECT (ST_Dump(ST_GeneratePoints(geom, 2000))).geom AS geom FROM peru WHERE name = 'Peru'
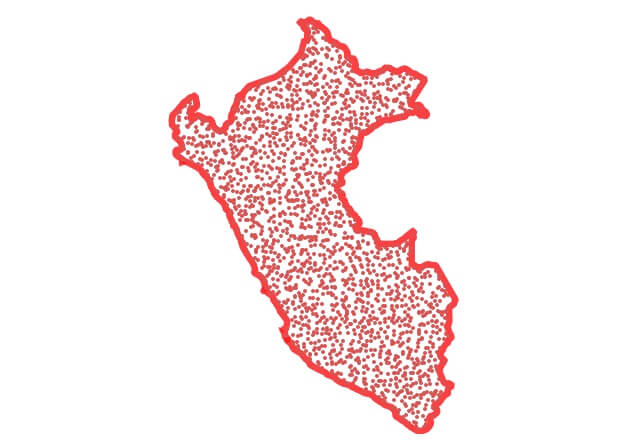
Agora, agrupe o campo de pontos, definindo o número de clusters para o número de partes em que você deseja dividir o polígono. Visualmente, agora você pode ver as divisões no polígono! Mas ainda precisamos obter linhas reais para representar essas divisões.
CREATE TABLE peru_pts_clustered AS SELECT geom, ST_ClusterKMmeans(geom, 10) over () AS cluster FROM peru_pts;
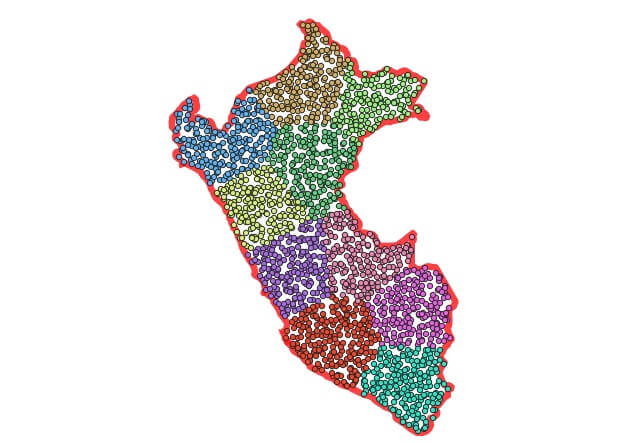
Primeiro, calcule o centroide de cada cluster de pontos, que será o centro de massa de cada cluster.
CREATE TABLE peru_centers AS SELECT cluster, ST_Centroid(ST_collect(geom)) AS geom FROM peru_pts_clustered GROUP BY cluster;
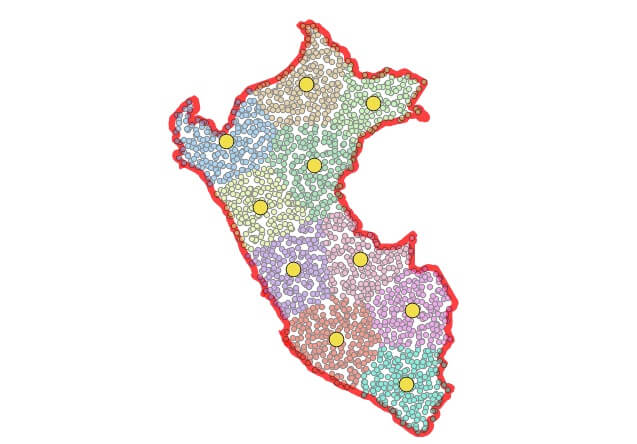
Agora, use um diagrama de voronoi para obter arestas de divisão reais entre os centróides do cluster, que acabam combinando de perto com os locais onde os clusters se dividem!
CREATE TABLE peru_voronoi AS SELECT (ST_Dump(ST_VoronoiPolygons(ST_collect(geom)))).geom AS geom FROM peru_centers;
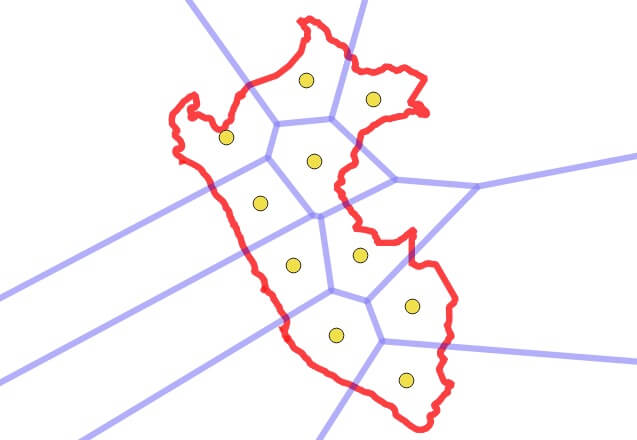
Finalmente, intercepte as áreas de voronoi com o polígono original para obter os polígonos de saída final que incorporam as bordas externas das linhas de divisão.
CREATE TABLE peru_divided AS SELECT ST_Intersection(a.geom, b.geom) AS geom FROM peru a CROSS JOIN peru_voronoi b;
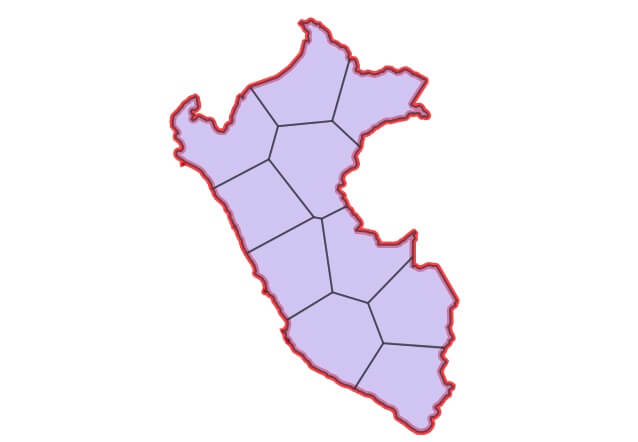
Feito!
Agrupar um campo de pontos para obter áreas praticamente iguais e, em seguida, usar o voronoi para extrair linhas divisórias reais são insights maravilhosos sobre o processamento espacial. A imagem final de todos os componentes do cálculo também é bonita.
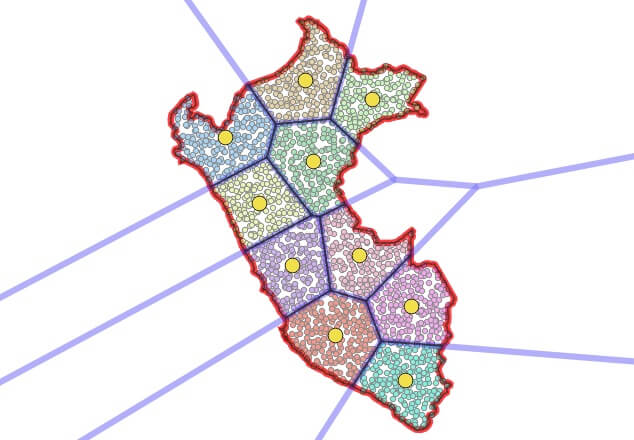
Não tenho 100% de certeza, mas talvez seja possível usar a técnica de Darafei para subdivisões ainda mais interessantes, como “mapa do Brasil subdividido em áreas de igual PIB”, ou “mapa de São Paulo subdividido em áreas de igual tamanho”, ou ainda a população ”gerando o campo de ponto inicial usando uma ponderação econômica ou demográfica”.
Este texto foi traduzido e adaptado do post original de Paul Ramsey no blog Clever Elephant.
Fonte: Blog Clever Elephant

